Prewitt Operator for Edge Detection

In the realm of image processing, the ability to detect edges is crucial for understanding and interpreting visual information. Among the pioneering techniques that have shaped this field is the Prewitt operator, a powerful algorithm developed by Judith M. S. Prewitt.

Renowned for its effectiveness in identifying gradients, the Prewitt operator not only laid the groundwork for modern edge detection methods but also continues to be a vital tool in various applications, from computer vision to medical imaging. In this article, we will explore the mechanics of the Prewitt operator, its historical significance, and its enduring relevance in today’s digital landscape.

Marker Effect – Interactive Preview

How does the Prewitt operator works?

The Prewitt operator is used to detect edges in images through convolution with two distinct filter masks: one for horizontal edges and another for vertical edges. This approach allows us to extract:

• Horizontal edges
• Vertical edges
• Edges in both directions

For more information on the process of convolution in image processing, you can refer to this article on image convolution.

The coefficients of the Prewitt masks are as follows:

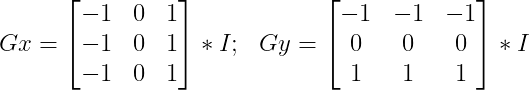
Like other gradient detection operators, this one also has a separable property.

For example we can represent Gx as:

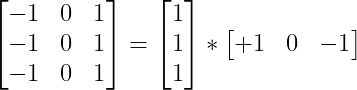
We apply both masks to each pixel of the image. In this way we find the difference in the intensity levels of the neighboring pixels in both directions. The result of this operation determines the so-called first derivative of the signal (image).

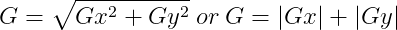
Using the following equation we can calculate the orientation of the edge of each pixel. This parameter allows very fast thinning of the resulting contour lines by the non-maximum suppression algorithm:

Example

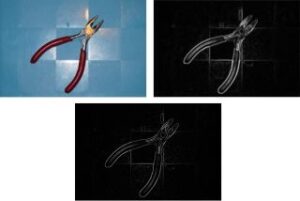
The image below is an example result of Prewitt edge detector. To reduce noise in the picture, it is enhanced with Gaussian blur prior the edge detection process.

Other gradient operators

Gradient detection is a common task in image analysis and there are alternative operators for this purpose. Some of which are:

• Sobel-Feldman operator
• Scharr operator

What is the difference between Prewitt and Sobel?

Gradient differentiation operators such as Prewitt, Sobel, and Scharr operate on the same fundamental principle. They all utilize separable kernels to approximate the gradient of an image.

The key difference lies in how these filters assign weights to the pixels within their masks. The Prewitt filter applies equal weight to all pixels under the mask, while both Sobel and Scharr assign greater weight to pixels closer to the center of the mask, thereby emphasizing the central pixel’s contribution more significantly.

Source code

Here are some related articles that provide programming approaches to implementing edge detection techniques:

• Simple Image class template in C++
• Prewitt operator in pure JavaScript
• Image edge detection with OpenGL / WebGL

These resources offer practical examples and code snippets to help you understand and implement the concepts discussed.

Gradient Detection Online

On our online test page you can see and compare the most popular gradient detectors for free without any installation, registration or whatever.