Median Filter – edge preserving filter tutorial

The Median filter is a nonlinear noise reduction technique that is widely used in image processing. It is very effective in cases of salt and paper noise (impulsive noise) and speckle noise.

However, in cases of high noise levels, its performance becomes compatible with Gaussian blur filtering.

The main advantage of median filter is that it can blur and reduce the noise levels while retains edges. This feature makes it an appropriate preliminary step for further computer vision tasks such as edge detection and extraction.

An important note is that this filter has the effect to round existing corners and is not suitable for corner detection.

---

How Median Filter works?

The Median filter works with a sliding window that pass through each signal entry one by one. At each point numerically sort the list of adjacent neighbors and then replace central value with the middle one from the list. The classical algorithm uses sorting, which is not much efficient and may lead to bigger execution delay. Thus in attempts for optimization there are several different techniques for finding the middle value.

How to find the median value?

• Array sorting – this is a classical algorithm where we sort the values below the median kernel and as a result we use the value in the middle
• Selection algorithm – it is acceptable to use partial sorting or other selection method, since the goal is simply to find the middle value.
• Histogram medians – at window movement we can update histogram with pixel changes and use it further to resolve the median value

The following picture displays an example of 3×3 sliding window and how the algorithm process current pixel.

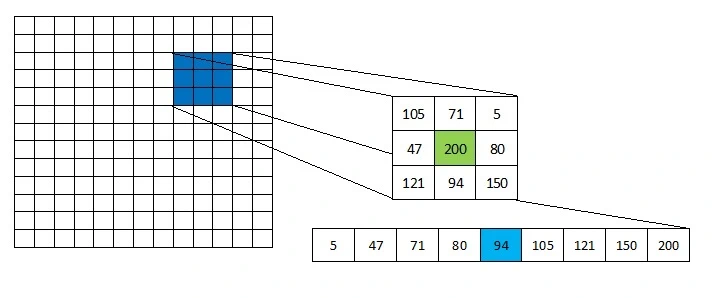
The image above show how the sliding mask represents the matrix as 1D array of pixel values. To extract the middle value the algorithm sorts the neighbors array . Then the middle value replaces the central pixel.

Algorithm source code

The below code snippet shows how we can implement median filtering with different kernel size via pure JavaScript. Note that although this approach is almost independent of the size of the kernel, it uses only CPU power. Because of this it does not allow high processing speed compared to similar GUP filters.

function median(pixels, size, colors) {
  var d = pixels.data;
  var buff = new pixels.data.constructor(new ArrayBuffer(pixels.data.length));
  var w = pixels.width;
  var h = pixels.height;
  const bpr = w*4; // Bytes per row

  if (size < 3) return;

  const ms = Math.floor(size / 2);
  const mc = Math.floor((size*size) / 2);

  // Find the middle value by histogram traversal
  function getMiddle(h, n){
    for (var count = h[0], i = 1; i < 256; i++, count += h[i]){ 
      if (count >= n){ return i; }
    }
    return 255;
  }
  colors = colors || 3;
  for (var i, j, c = 0; c < colors; c++){
    var srcIt, dstIt, l;
    for (i = ms; i < h - ms; i++) {
      var hist = new Uint16Array(256);
      const offset = (i - ms)*bpr + c;
      
      for (var ii = (i - ms)*bpr; ii <= (i + ms)*bpr; ii+=bpr){
        for (var jj = c; jj < (ms*2)*4 + c; jj+=4){
          hist[d[ii + jj]]++;
        }
      }

      for (j = ms, dstIt = i*bpr + j*4 + c; j < w - ms; j++, dstIt+=4){
       
        // Add rigtmost values to the histogram
        for (srcIt = offset + (j + ms)*4, 
          l = srcIt + bpr*size; srcIt < l; srcIt+=bpr){
          hist[d[srcIt]]++;
        }

        buff[dstIt] = getMiddle(hist, mc);
        // Remove leftmost values to the histogram
        for (srcIt = offset + (j - ms)*4, 
          l = srcIt + bpr*size; srcIt < l; srcIt+=bpr){ hist[d[srcIt]]--; } 
      } 
    } 
  } if (colors > 1) {
    for (var i = 3; i < l; i+=4){
      buff[i] = 255;
    }
  } else {
    for (var i = 3; i < l; i+=4){
      buff[i] = 255;
      buff[i - 2] = buff[i - 1] = buff[i - 3];
    }
  }

  pixels.data.set(buff);

  return pixels;
}

---

Example app

Developers Portal

• Simple Image class template in C++
• Gaussian filter in OpenGL/WebGL

References

• Median Filtering – Ziv Yaniv

---