Gaussian blur is an essential part of many image processing algorithms. It serves to clear the noise in the images, as well as a general visual effect in various graphics software.
The following photo utility uses a Gaussian filter to blur images right in a web browser.
Interactive Preview: Online Image Blur
What is Gaussian blur?
Gaussian blurring is a non-uniform noise reduction low-pass filter (LP filter). The visual effect of this operator is a smooth blurry image. This filter performs better than other uniform low pass filters such as Average filter (Box blur).
How does Gaussian smoothing works?
Gaussian smooth is an essential part of many image analysis algorithms like edge detection and segmentation.
The Gaussian filter is a spatial filter that works by convolving the input image with a kernel. This process performs a weighted average of the current pixel’s neighborhoods in a way that distant pixels receive lower weight than these at the center.
The result of such low-pass filter is a blurry image with better edges than other uniform smoothing algorithms. This makes it a suitable choice for algorithms such as Canny edge detector.

The math equations below show how to calculate the proper weights of a Gaussian kernel.
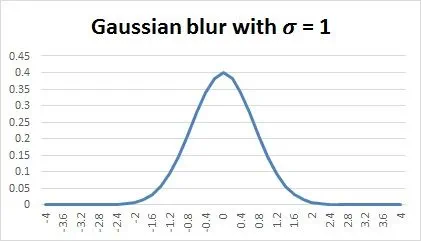
One dimensional Gaussian function
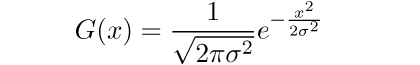
Two dimensional Gaussian function
The equation below (2) shows how to calculate two-dimensional Gaussian function:

Separable property
In practice, it is better to take advantage of the separable properties of the Gaussian function. This feature allows you to blur the picture in two separate steps.
This saves computing power by using a one-dimensional filtering as two separate operations. As a result, we achieve a fast blur effect by dividing its execution horizontally and vertically.
Features and applications
The list below provides a brief summary of the characteristics of the Gaussian filter:
- It is a separable filter – this property can save significant computing power
- Preferable choice for edge detection – using “weighted” masks makes it better than some uniform blur filters
- Multiple iterations with a given filter size have the same blur effect as the larger one
- Useful as a pre-processing step for image size reduction
Discrete Approximations
In many cases it is enough to use an approximation of Gaussian function. Below are examples of popular filtering masks that we often use in computer vision.
Separable Filter with Size 3×3
![Discrete approximation of Gaussian filter with kernel size 3x3 $\displaystyle{K}=\frac{1}{{16}}{\left[\begin{matrix}{1}&{2}&{1}\\{2}&{4}&{2}\\{1}&{2}&{1}\end{matrix}\right]}={\left[\begin{matrix}{1}&{2}&{1}\end{matrix}\right]}\frac{1}{{4}}\ast{\left[\begin{matrix}{1}\\{2}\\{1}\end{matrix}\right]}\frac{1}{{4}}$](https://fiveko.com/wp-content/uploads/2017/08/gauss_blur_3x3.png)
Separable Filter with Size 5×5
![Discrete approximation of Gaussian filter with kernel size 5x5 $\displaystyle{K}=\frac{1}{{256}}{\left[\begin{matrix}{1}&{4}&{6}&{4}&{1}\\{4}&{16}&{24}&{16}&{4}\\{6}&{24}&{36}&{24}&{6}\\{4}&{16}&{24}&{16}&{4}\\{1}&{4}&{6}&{4}&{1}\end{matrix}\right]}=\frac{1}{{16}}{\left[\begin{matrix}{1}&{4}&{6}&{4}&{1}\end{matrix}\right]}\ast\frac{1}{{16}}{\left[\begin{matrix}{1}\\{4}\\{6}\\{4}\\{1}\end{matrix}\right]}$](https://fiveko.com/wp-content/uploads/2017/08/gauss_blur_5x5.png)
Note that when converting continuous values to discrete ones, the total sum of the kernel will be different than one. This leads to brightening or darkening of the picture, so in practice we normalize the kernel. We achieve this by dividing each of its elements by the sum of all of them.
Gaussian Filter example code
The table below provides links to sample source code in various programming languages and technologies:
| Link | Description |
|---|---|
| Gaussian filter in pure JavaScript | Use native JavaScript to implement blur effect on images and pictures. No dependencies and third party libraries. |
| Gaussian filter in OpenGL (WebGL) | Implement image blur filter using WebGL/OpenGL technology. Simple and fast image filtering using GPU. |
Image Filtering Online
You can use various image editing and analysis tools for free, here online in your browser. No registration, download and without watermarks.

WEB APPLET
See how it works in the browser!





