The Hough Transform is a method to find shapes in an image. The classical transformation is initially designed to identify lines in the image. Later the transform extends to identify different kind of shapes such as circles, ellipses and even arbitrary objects.
What is Hough Transformation?
Hough’s transformation uses a voting scheme in parameter space, so that it populates an “accumulator” with present edge points. The voting procedure helps to improve the feature detection accuracy and overcome cases of missing or noisy feature parts.
Тhe following steps briefly describe the Hough’s algorithm:
- Extract edges using e.g. Sobel edge detector
- Choose desired transformation e.g. line transform or circle transform
- Iterate through the image and populate the accumulator using the transform from previous step
- Search for the local maximum values inside the accumulator space
Find lines in an image
Hough linear transformation is a well-known method for detecting straight segments in images. A line that pass through a point x,y can be represented using the Polar coordinate system by the following equation:
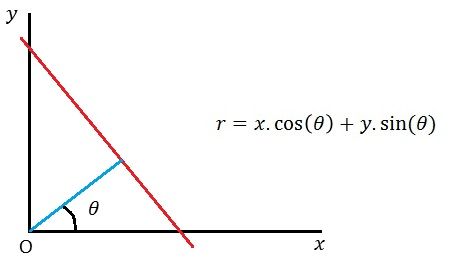
The equation above helps to calculate and plot each family of lines that pass through every significant edge pixel (e.g. x0,y0). As a result each such pixel helps to fill the Polar accumulator (r, theta) with proper radius per all possible angles. Finally, we retrieve all possible lines by looking for the peaks of the accumulator.
Note that the lines we receive do not contain length information. Therefore we need further processing to match the exact parts of the image with corresponding lines.
Discover circles in an image
The math behind the Hough circle transform is similar to this used for lines detection described above. The equation below determines the voting accumulator cells:
x = R*cos(phi);
y = R*sin(phi);
Where R is the radius of the searched circles and phi is angle in radians from 0-2PI.
Circles Transform on HTML5 2D Canvas
In order to optimize the algorithm execution and reduce needed time we use a pre-calculated lookup table (LUT) with x and y values respectively. The JavaScript code snippet below shows the lookup table creation:
// Compute the circle kernel (LUT)
var kernel = [{x: ~~(r*Math.cos(0)), y: ~~(r*Math.sin(0))}];
for (var i = 1; i < 380; i++){
var phi = i*Math.PI/180;
var x = ~~(r*Math.cos(phi));
var y = ~~(r*Math.sin(phi));
var last_element = kernel[kernel.length - 1];
if (last_element.x != x || last_element.y != y)
kernel.push({x: x, y: y});
}Next step is to loop through image pixels and execute the voting procedures. We find the overall sum at each pixel using the lookup table. As a reference, see the code fragment below:
// Create buffer using pixels.data ctor
var buff = new pixels.data.constructor(new ArrayBuffer(pixels.data.length));
var data = pixels.data;
var w = pixels.width - r;
var h = pixels.height - r;
var i, j, bpr = pixels.width*4;
for (i = r; i < h; i++){
for (j = r; j < w; j++){
var sum = 0, l = kernel.length;
for (var k = 0; k < l; k++){
var x = j + kernel[k].x;
var y = i + kernel[k].y;
sum += data[bpr*y + x*4]; // Assume it's grayscale
}
const pos = bpr*i + j*4;
buff[pos + 0] = buff[pos + 1] = buff[pos + 2] = ~~(sum / l);
buff[pos + 3] = 255;
}
}
pixels.data.set(buff);
Circles detector with WebGL
The following OpenGL fragment shader implements a
precision mediump float;
// our texture
uniform sampler2D u_image;
uniform vec2 u_textureSize;
uniform float u_r;
#define M_PI 3.14159265359
#define PHI_STEP M_PI/180.0
void main() {
vec2 onePixel = vec2(1.0, 1.0) / u_textureSize;
vec2 textCoord = gl_FragCoord.xy / u_textureSize;
vec4 sum = vec4(0.0);
float phi = 0.0;
for (int i = 0; i < 360; i++)
{
phi += PHI_STEP;
sum += texture2D(u_image, textCoord + onePixel*vec2(u_r*cos(phi), u_r*sin(phi)));
}
gl_FragColor = vec4(vec3(sum / 360.0), 1.0);
}This source code snippet is part of our online image processing library where you can find the full implementation and many other algorithms.




