The Mean filter is a linear low-pass blur photo filter where each pixel in the output image has average value of its neighboring pixels. The algorithm is also famous as Box blur and performs as convolution with average blur mask.
How does average filter works?
Even though the modern camera devices provide pretty good quality, often pictures are noisy. In such cases a common technique is to use low-pass filter to prevent high frequency noise artifacts.
We often call the Mean filter a “blurring” or “smoothing” filter, because the result is a blurry image.
In some articles you may find this operator as average filter, since for any pixel from image it takes the average value across its neighbors.
Like the Gaussian operator, this filter is also separable, so usually at a larger size it is better to run it once for rows and once for columns.
![$\displaystyle{K}=\frac{1}{{9}}{\left[\begin{matrix}{1}&{1}&{1}\\{1}&{1}&{1}\\{1}&{1}&{1}\end{matrix}\right]}=\frac{1}{{3}}{\left[\begin{matrix}{1}&{1}&{1}\end{matrix}\right]}\ast\frac{1}{{3}}{\left[\begin{matrix}{1}\\{1}\\{1}\end{matrix}\right]}$](/wp-content/uploads/2017/08/mean_filter_3x3.png)
Moving Averages
In addition to mean filter separation it is possible to apply additional optimization called “moving averages”. This will reduce its complexity further to O(1).
The following steps describe the process:
- Iterate through each row/column in a single pass
- For the first pixel use the whole kernel size and calculate the sum and write the mean as output
- For each next pixel use the sum from the previous step and subtract values which are no longer under the kernel.
- Add the new values that come under the mask
- Calculate the average sum and write it as output

Iterative Average filter (Box Blur)
We base our algorithm on the fact that Gaussian filter approximates well by multiple iterations of Average filter.
Equation (1) describes the standard deviation of mean filter with size n, since it corresponds to uniform probability distribution. In case of multiple iterations m, the standard deviation is result from equation 2.
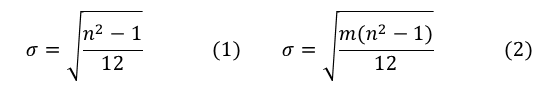
Thus in order to calculate number of iterations m for known kernel size (e.g. n=3) and provided sigma, the equation could be represented as following:

This iterative approach is suitable for fast parallel computing (GPU), where we can use WebGL to make a quick blur effect on photos.
Source Code for fast Image blur
See it Online
WEB APPLET
See how it works in the browser!

Resources
- Geometric mean filter – Wikipedia



