Harris Corner Detector is a popular computer vision algorithm used to detect key points in images and video. Corners are important features of the image, as they provide useful information for detecting objects and scenes.
Common applications
Key points extraction is a common image analysis task where Harris operator fits well. The algorithm is robust and is accurate in distinguishing edges and corners.
Some common uses of it are:
- Image classification
- Objects recognition
- Objects tracking in video sequence
- Image alignment and stitching for panoramic image creation

How does Harris Corner Detector works?
Corners are regions located between two dominant image edges with different direction. This means that at such points there will be large variations in intensity in many directions.
Harris puts this fact into action so that his operator finds significant changes in image gradient for a local area (window). The basic principle is that it calculates the difference in the displacement of the kernel in all directions.
When the window is above a linear gradient segment, changes in direction will reduce the result. Otherwise, when the window is over a corner, movements in each direction will increase the intensity change.

Basically the Harris corner detector algorithm will have the following steps:
- Edge detection – for image derivatives calculation it is appropriate to use Sobel edge detector
- Image smoothing – frequently this step uses Gaussian or Mean filters
- Harris measure computation
- Non-maximum suppression
- Feature points thresholding
Harris response calculation
A movable image patch at position (x, y) shifts with defined offset (dx,dy):
![$\displaystyle{M}=\sum_{{{x},{y}}}{W}{\left({x},{y}\right)}{\left[\begin{matrix}{I}{x}^{2}&{I}{x}{I}{y}\\{I}{x}{I}{y}&{I}{y}^{2}\end{matrix}\right]}$](/wp-content/uploads/2018/08/harris_corners.png)
The Harris corner score is used to determine if the current position contains a corner or not:
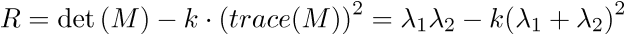
Matrix trace calculation
In linear algebra the det(M) stands for a square matrix determinant. To calculate determinant of 2×2 matrix use the following eqution:
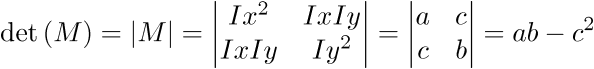
Matrix trace calculation
In linear algebra the trace(M) of a square matrix is the total sum of the main diagonal. To calculate the trace of the Harris matrix use the following equation:
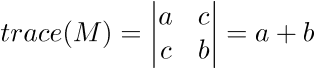
Harris result image map
Finally, the algorithm creates a gray-scale map image where the bright areas are the corners.

Source Code
The proposed algorithm uses OpenGL Shading Language (GLSL) to provide parallel execution and good performance.
Derivatives calculation
First of all we calculate image gradients in horizontal and vertical direction. As a result our algorithm stores the derivatives as in below snippet.
float dx = length((GET_PIXEL(-1, -1)*u_kernel[0] +
GET_PIXEL(-1, 0)*u_kernel[1] +
GET_PIXEL(-1, +1)*u_kernel[2]) -
(GET_PIXEL(+1, -1)*u_kernel[0] +
GET_PIXEL(+1, 0)*u_kernel[1] +
GET_PIXEL(+1, +1)*u_kernel[2]));
float dy = length((GET_PIXEL(-1, -1)*u_kernel[0] +
GET_PIXEL(0, -1)*u_kernel[1] +
GET_PIXEL(+1, -1)*u_kernel[2]) -
(GET_PIXEL(-1, +1)*u_kernel[0] +
GET_PIXEL(0, +1)*u_kernel[1] +
GET_PIXEL(+1, +1)*u_kernel[2]));
gl_FragColor = vec4(dx*dx, dy*dy, dx*dy, 1.0);
How to generate key-points map
Next step is to compute Harris corner score at each image pixel and generate key-points map.
#define DET(_p) ((_p).x*(_p).y - (_p).z*(_p).z)
#define TRACE(_p) ((_p).x + (_p).y)
vec4 p = (GET_PIXEL(0, 0) + GET_PIXEL(-1, -1) +
GET_PIXEL(-1, 0) + GET_PIXEL(-1, 1) +
GET_PIXEL( 0, 1) + GET_PIXEL( 1, 1) +
GET_PIXEL( 1, 0) + GET_PIXEL( 1, -1) +
GET_PIXEL( 0, -1)) / 9.0;
float k = 0.04;
float R = DET(p) - (k * (TRACE(p)*TRACE(p)));
How to extract dominant feature point?
Similar to Hough’s transformation, Harris’s algorithm yields multiple detection results in neighboring locations. Therefore, it is usually required to apply fast peak detection algorithm and to isolate only prominent key points.
Online App
Visit our online sample page to see the Harris corners detector in action.
WEB APPLET
See how it works in the browser!

Source Code
- Fast Peak Detection for 2D Images via GL Shader
- Image edge detection with simple JavaScript
- Fast edge detection with OpenGL/WebGL



