The Sobel filter (also called Sobel-Feldman operator) is an edge detection algorithm, that results in image emphasizing edges. Computer vision apps often use this image processing technique to extract the objects contours.
What is Sobel filter?
The Sobel-Feldman operator is a separable edge detection filter. It is named after its discoverers – Irwin Sobel and Gary Feldman.
Like the Prewitt operator, the Sobel filter consists of two 3×3 convolution masks. From a computational point of view, it is relatively cheap to implement.
Application
The Sobel operator is applicable in many computer vision algorithms, some of which are:
Theory
The Sobel masks are with such design that they provide maximum value at horizontal or vertical edge orientation. Both masks have the same coefficients as they are rotated 90 degrees to each other. Occasionally it is desirable to retrieve only one of the gradient orientation – horizontal or vertical.
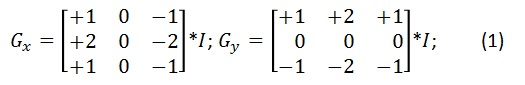
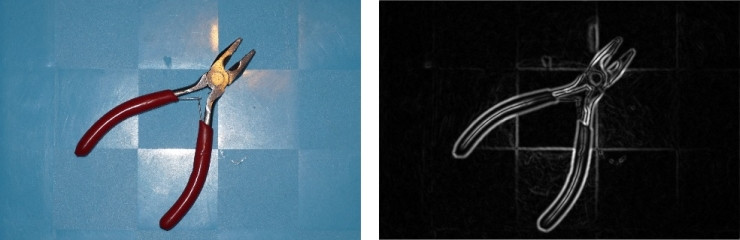
The image below is an example result of a Sobel operator, where we can see clear outlines of the objects.
Preprocessing
Typically, edge recognition results are easily affected by noise in the image. Because of this it is commonly recommended to apply some low-pass filter like Gaussian.
Smoothing filters often smudge the edges as well. Therefore, many articles suggest the use of nonlinear edge-preserving filtering. Examples of such filters are: Symmetric Nearest Neighbor or Median filter.
How the Sobel filter works?
The Sobel filter works through a simple 3×3 convolution, so it is efficient for both CPU and GPU computations. The Sobel kernels are separable, which is an additional optimization option.
![$\displaystyle{G}{x}={\left[\begin{matrix}+{1}&{0}&-{1}\\+{2}&{0}&-{2}\\+{1}&{0}&-{1}\end{matrix}\right]}={\left[\begin{matrix}{1}\\{2}\\{1}\end{matrix}\right]}\ast{\left[\begin{matrix}{1}&{0}&-{1}\end{matrix}\right]}$](https://fiveko.com/wp-content/uploads/2017/08/Sobel_horizontal.png)
![$\displaystyle{G}{y}={\left[\begin{matrix}+{1}&+{2}&+{1}\\{0}&{0}&{0}\\-{1}&-{2}&-{1}\end{matrix}\right]}={\left[\begin{matrix}{1}\\{0}\\-{1}\end{matrix}\right]}\ast{\left[\begin{matrix}{1}&{2}&{1}\end{matrix}\right]}$](https://fiveko.com/wp-content/uploads/2017/08/Sobel_vertical.png)
Each image pixel is processed by each kernel in order to produce the final gradient value using equation (2). Additionally to gain performance it is acceptable to use the sum of absolute directional values as in equation (3).
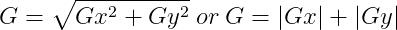
After calculating the vertical and horizontal gradients, we can also extract the edge orientation:

We can note that usually edge detection creates thick contours of the object. In many cases, this is not very useful for object recognition and we need to apply additional processing.
To extract thin and strong edges of the image, we use the gradient magnitude and orientation. These parameters are sufficient to do edge thinning by non-maximum suppression.
Source code
The Sobel-Feldman filter is a common technique in computer graphics. In the following articles you can find implementation in different programming languages:
Edge Detection App
You can see how the Sobel filter works in our online image analysis demo.
References
- Irwin Sobel, 2014, History and Definition of the Sobel Operator